以下为《条件概率ppt》的无排版文字预览，完整格式请下载

下载前请仔细阅读文字预览以及下方图片预览。图片预览是什么样的，下载的文档就是什么样的。

条件概率1、概念

2、乘法定理

3、全概率公式

4、贝叶斯公式条件概率的概念 概念：

设A、B是两个事件，且P（A）>0，称

P（B|A）=P（AB）/P(A)

为在事件A发生条件下事件B发生的条件概率

条件概率例题某种灯泡的使用寿命为2000小时的概率为0.85，超过2500小时的概率为0.35，若某个灯泡已经使用了2000小时，那么它能使用超过2500小时的概率为多少

解：记灯泡的使用寿命为2000小时的事件为A，超过2500小时的事件为B，则P(B│A)= = 0.35 0.85 = 3 17

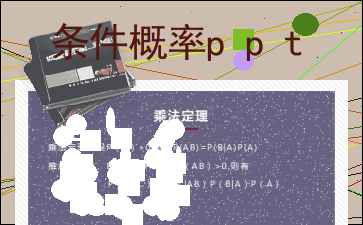
??(????) ??(??) 乘法定理乘法定理：设P（A）>0,则有P(AB)=P(B|A)P(A)

推广 ：设A、B、C为事件，且P（AB）>0,则有

P（ABC）=P（C|AB）P（B|A）P（A）

乘法定理例题设某光学仪器厂制造的透镜，第一次落下时打破的概率为1/2,若第一次落下未打破，第二次落下打破的概率为7/10，若前两次 内容过长，仅展示头部和尾部部分文字预览，全文请查看图片预览。 =0.01,P(A│ ?? 3 )=0.01

P(A)=P(A│ ?? 1 )P( ?? 1 )+P(A│ ?? 2 )P( ?? 2 )+P(A│ ?? 3 )P( ?? 3 )

=0.02×0.3+0.01×0.5+0.01×0.2=0.013贝叶斯公式定理 设实验C的样本空间为S，B为C的事件，A1、A2、...、An为C的一个划分，且P（Ai）>0，P（B）>0,则

P（Ai|B）=P(B|Ai)P(Ai)/P(B|A1)P(A1)+P（B|A2）P（A2）+...+P（B|An）贝叶斯例题对以往数据分析结果表明当机器调整良好时，产品的合格率为98%，而当机器发生某种故障时，其合格率为55%。每天早上机器开动时，机器调整良好的概率为95%。试求已知某日早上第一件产品是合格品时，机器调整良好的概率是多少？

解：设 A 为事件“产品合格”, B 为事件“机器调整良好”

已知 P ( A│B )=0.98, P ( B )=0.95, P ( A│ ?? )=0.55, P ( ?? )=0.05,所求的概率为 P ( B│A )．由贝叶斯公式

P ( B│A)= ??(??│??)??(??) ??(??│??)??(??)+??(??│ ?? )??( ?? ) = 0.98×0,95 0.98×0.95+0.55×0.05 =0.97

所以当生产出的第一件产品是合格品时，此时机器调整良好的概率为0.97.[文章尾部最后300字内容到此结束,中间部分内容请查看底下的图片预览]

以上为《条件概率ppt》的无排版文字预览，完整格式请下载

下载前请仔细阅读上面文字预览以及下方图片预览。图片预览是什么样的，下载的文档就是什么样的。